Quand les maths prédisent le temps

En 1904, le scientifique norvégien Wilhelm Bjerknes proposa un modèle mathématique destiné à prévoir l’évolution des océans et de l’atmosphère. Il posa ainsi les bases à la fois de la météorologie (prévisions à court terme) et de la climatologie (prévisions à long terme).

Ce modèle a cependant longtemps attendu son heure de gloire. En cause : sa complexité mathématique et le challenge que représente le calcul effectif de ses solutions. Au sortir de la Seconde Guerre mondiale, le développement de l’informatique permit enfin de calculer les premières prévisions météorologiques convaincantes. Les théorèmes se feront cependant encore attendre, car c’est seulement entre 1992 et 2007 que fut montré que ce modèle a bien une et une seule solution. Un résultat rassurant pour un modèle prédictif dont on ne sait que calculer des solutions approchées, faute de formule explicite pour la solution exacte. C’est l’histoire de ce modèle mathématique, de son origine physique, de son utilisation numérique et de sa justification mathématique en tant que modèle prédictif que nous allons raconter.

Pour aller plus loin

Pourquoi la météo se trompe-t-elle si souvent ?

Convertir l’atmosphère sous la forme d’équations

Au début du vingtième siècle, Wilhelm Bjerknes, alors professeur de mécanique appliquée et de mathématiques à l’université de Stockholm, conçoit un plan d’attaque pour prévoir l’évolution du temps. D’abord, obtenir une connaissance suffisamment précise de l’état de l’atmosphère. Ensuite, utiliser les lois les plus pertinentes de l’hydrodynamique et de la thermodynamique pour déterminer la dynamique de sept quantités cruciales : la pression, la température, la densité, l’humidité et la vitesse de l’air dans les trois directions de l’espace. Comme s’il avait eu l’intuition que notre environnement était à soigner, Bjerknes utilisa les termes « diagnostique » et « pronostique » pour désigner ces deux étapes.

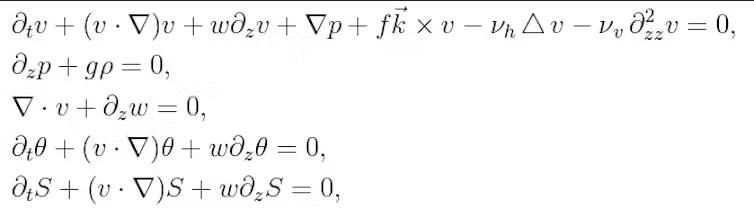
Les équations en jeu, appelées équations primitives, sont des équations aux dérivées partielles. Cela signifie qu’elles font intervenir l’évolution dans le temps et dans l’espace des sept grandeurs physiques clés. Ces équations sont déterministes, ce qui signifie qu’elles ne contiennent pas d’aléatoire. Elles sont de plus non linéaires. Ainsi, une petite imprécision anodine à un instant donné dans les mesures peut s’amplifier terriblement par la suite et fausser complètement les prévisions. C’est là que réside la difficulté de faire des prévisions pertinentes à long terme.

Bjerknes, qui fonda ensuite l’Institut de géophysique de Bergen, fit de nombreux émules et fut sollicité par l’armée norvégienne pour fournir des prévisions météorologiques stratégiques lors de la Première Guerre mondiale.

Le développement clé de l’informatique pour réussir à faire des prédictions

Mais à cette époque, l’informatique n’était pas suffisamment développée pour permettre des prévisions météorologiques efficaces. Ce n’est qu’en 1947 que, sous l’impulsion du mathématicien John von Neumann, le premier superordinateur développé aux États-Unis, nommé ENIAC, réalisa les premières prévisions météorologiques convaincantes.

Mathématiquement, l’étude de ce problème a débuté au début des années 1990, grâce à une série d’articles des mathématiciens Jacques-Louis Lions, Roger Temam et Schouhong Wang. L’enjeu est simple : prouver que ces équations d’évolution ont bien une et une seule solution, définie pour un temps que l’on souhaite le plus long possible, pour le plus grand nombre de données initiales possibles. Dans le cas contraire, cela signifierait qu’un calcul numérique pourrait fournir aussi bien une approximation de la solution pertinente physiquement qu’une solution qui n’aurait rien à voir avec la réalité des faits ! Les simulations informatiques ne seraient alors pas toujours fiables, quelle que soit la puissance de la machine utilisée.

La rotation de la Terre, les aspects thermodynamiques, le transport et la diffusion de la salinité dans les océans sont autant de phénomènes à prendre en compte dans l’analyse mathématique. En revanche, la faible profondeur des océans ainsi que la faible hauteur de l’atmosphère par rapport au rayon de la Terre conduisent à négliger le mouvement vertical de l’eau ou de l’air, ce qui permet de simplifier le modèle mathématique.

S’assurer de la pertinence du modèle

Les équations primitives se situent ainsi en quelque sorte entre les dimensions deux et trois ! Cette observation permit en 2007 à deux mathématiciens, Chongsheng Cao et Edriss Titi, de prouver qu’à une donnée initiale régulière, c’est-à-dire sans variation brutale, est associée une unique solution régulière, bien définie pour tous les instants. De plus, le résultat montre aussi que la sensibilité au moindre changement des conditions initiales, si elle est bien réelle, ne conduit pas, par la suite, à des sauts brutaux, de température ou d’humidité, par exemple, au cours du temps. Ce dernier point est particulièrement appréciable compte tenu de ce que l’on ne peut bien sûr pas espérer connaître exactement l’état du système à un instant précis. La viabilité du modèle comme outil prédictif est ainsi, théoriquement, bien assurée.

Depuis, de nombreux travaux ont été réalisés pour étendre ce résultat marquant à des modèles plus sophistiqués, de plus en plus proche de la réalité. Une autre problématique d’actualité est la comparaison des différents modèles, en fonction des paramètres physiques qu’il modélise. Le but est pour le chercheur de pouvoir choisir en conscience à quel modèle se fier, arbitrant, en fonction de sa puissance de calcul, entre complexité et pertinence.

Enfin, un doux rêve est d’explorer, au moins théoriquement, la possibilité d’agir sur de tels systèmes. D’ailleurs, on attribue, lors d’une de ses conférences, les propos suivants à John von Neumann : « Le climat est peut-être plus facile à contrôler qu’à prédire ». La théorie mathématique de la contrôlabilité, qui explore justement les possibilités de modifier les systèmes d’évolution par une action ciblée, est pourtant encore loin, aujourd’hui, de couvrir le cas des équations primitives.

Bien qu’âgées de 120 ans, et amplement utilisées dans des simulations informatiques depuis quatre-vingts ans, les équations primitives sont ainsi encore dans leur adolescence du point de vue de leur compréhension mathématique.

Franck Sueur, Professeur en Mathématiques, Université de Bordeaux

Cet article est republié à partir de The Conversation sous licence Creative Commons. Lire l’article original.

Vous voulez tout savoir sur la mobilité de demain, des voitures électriques aux VAE ? Abonnez-vous dès maintenant à notre newsletter Watt Else !