Courir ou marcher : quel est le plus efficace pour éviter d’être mouillé par la pluie ?

Vous êtes sorti, par un temps incertain, et la pluie se met à tomber alors que vous n’avez pas de parapluie. Le réflexe est de se pencher en avant et d’accélérer le pas, n’est-ce pas ? C’est ainsi qu’on a le sentiment qu’on se mouillera le moins. Il se peut même que l’on accepte de se mouiller plus à condition que cela dure moins longtemps.

Ce comportement est-il justifié ? Peut-on faire un modèle qui permette de répondre à cette question de la plus haute importance ? En particulier, la quantité d’eau reçue dépend-elle de la vitesse ? Existe-t-il une vitesse telle que la quantité d’eau reçue, pour aller d’un lieu à un autre, soit minimale ?

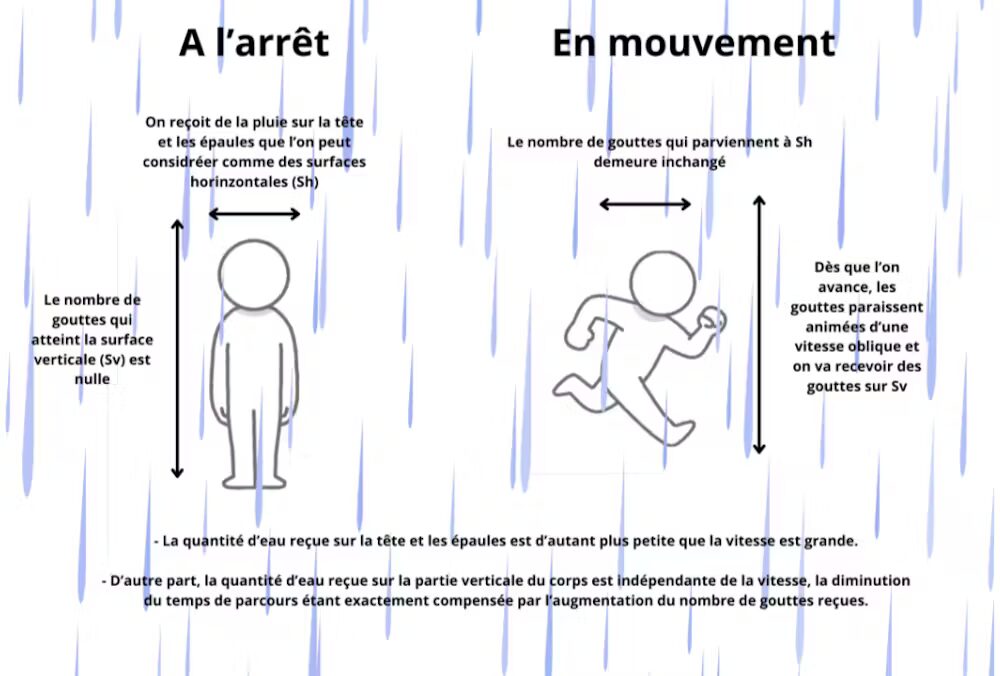
Faisons simple, tout en gardant les éléments importants de la situation. Considérons une pluie homogène qui tombe verticalement. Schématiquement, on peut considérer que le marcheur présente à la pluie des surfaces verticales (le devant et l’arrière du corps) et des surfaces horizontales (la tête et les épaules).

Considérons d’abord les surfaces verticales. En avançant, le marcheur va à la rencontre des gouttes : plus il va vite, plus il va en recevoir. De son point de vue, les gouttes tombent en oblique, avec une composante de vitesse exactement égale à sa propre vitesse de marche : plus il va vite, plus il va recevoir de gouttes. Oui, mais pour aller d’un point à un autre, il va mettre moins de temps, et d’autant moins qu’il va vite ! On voit donc que les deux effets se compensent exactement : plus de gouttes par unité de temps, mais moins de temps passé sous la pluie.

Qu’en est-il des surfaces horizontales ? Quand le promeneur est immobile, il ne reçoit la pluie que sur ces surfaces. Quand on le regarde avancer, on voit qu’il reçoit des gouttes qui, auparavant, lui passaient devant, mais il ne reçoit plus des gouttes qui passent maintenant derrière lui : au total, par unité de temps, il reçoit, sur ces surfaces horizontales, une quantité indépendante de sa vitesse de marche. Mais comme la durée totale de la marche diminue quand la vitesse augmente, la quantité d’eau reçue sur les surfaces horizontales sera plus faible.

Au total, on a donc bien raison d’accélérer le pas.

En apprendre plus

Pétrichor : la pluie a-t-elle une odeur ?

Courir ou marcher face à la pluie ? Les maths à la rescousse

Pour celles et ceux qui aiment un traitement mathématique des choses, voici de quoi les satisfaire :

Désignons par ρ le nombre de gouttes par unité de volume, et par a leur vitesse verticale. Désignons par Sh la surface horizontale de l’individu, et par Sv sa surface verticale.

Si l’on est immobile, on ne reçoit de la pluie que sur la tête et les épaules, c’est donc la quantité d’eau qui arrive sur la surface Sh.

Même si la pluie tombe verticalement, du point de vue du promeneur qui avance à la vitesse v, elle arrive de façon oblique, selon une direction qui dépend de la vitesse v.

Pendant un intervalle de temps T, une goutte parcourt une distance a.T. Donc, toutes les gouttes qui se trouvent à une distance inférieure vont atteindre cette surface : ce sont les gouttes qui se trouvent dans le cylindre de base Sh et de hauteur a.T, soit :

ρ.Sh.a.T.

Comme nous l’avons vu, dès que l’on avance, les gouttes paraissent animées d’une vitesse oblique qui résulte de la composition de la vitesse a et de la vitesse v. Le nombre de gouttes qui parviennent à Sh demeure inchangé, car la vitesse v est horizontale, donc parallèle à Sh. En revanche, le nombre de gouttes qui atteint la surface Sv, nul lorsque le promeneur était immobile, est maintenant égal au nombre de gouttes contenues dans un cylindre (horizontal) de base Sv et de longueur v.T, car cette longueur représente bien la distance horizontale parcourue par les gouttes pendant cet intervalle de temps.

Au total, le promeneur reçoit un nombre de gouttes donné par l’expression :

ρ.(Sh.a + Sv.v). T

Il faut à présent tenir compte de l’intervalle de temps pendant lequel le promeneur va se mouiller. S’il doit parcourir une distance d à la vitesse constante v, l’intervalle de temps est donné par le rapport d/v (ce qui suppose évidemment v non nul !). En reportant dans l’expression ci-dessus, on obtient le résultat final :

ρ.(Sh.a + Sv.v). d/v = ρ.(Sh.a/v + Sv). d

Nous obtenons donc le double résultat suivant :

• D’une part, la quantité d’eau reçue sur la tête et les épaules est d’autant plus petite que la vitesse est grande.
• D’autre part, la quantité d’eau reçue sur la partie verticale du corps est indépendante de la vitesse, la diminution du temps de parcours étant exactement compensée par l’augmentation du nombre de gouttes reçues.

Moralité : on a bien raison de se pencher et de presser le pas ! Mais attention, se pencher augmente Sh : il faut donc que cette augmentation soit compensée par l’augmentation de la vitesse !

Jacques Treiner, Physicien théoricien, Université Paris Cité

Cet article est republié à partir de The Conversation sous licence Creative Commons. Lire l’article original.