Tout le monde a connu la galère du déménagement qui consiste à faire passer un canapé dans un couloir — une situation immortalisée dans la série Friends lors d’une scène passée la postérité. Eh bien, il est fort possible que cette difficulté cruciale pour l’humanité (en tout cas pour toute personne qui se lance dans un emménagement) n’en soit plus un.
Jineon Baek, chercheur postdoctorant à l’université Yonsei à Séoul, a fait sa thèse sur ce problème mathématique à l’université du Michigan, en avançant une proposition de résolution. Le 2 décembre, sa thèse a été mise en ligne en prépublication (donc encore non revue par des pairs mathématiciens) sur le site ArXiv.
Un canapé particulier, celui de Gerver
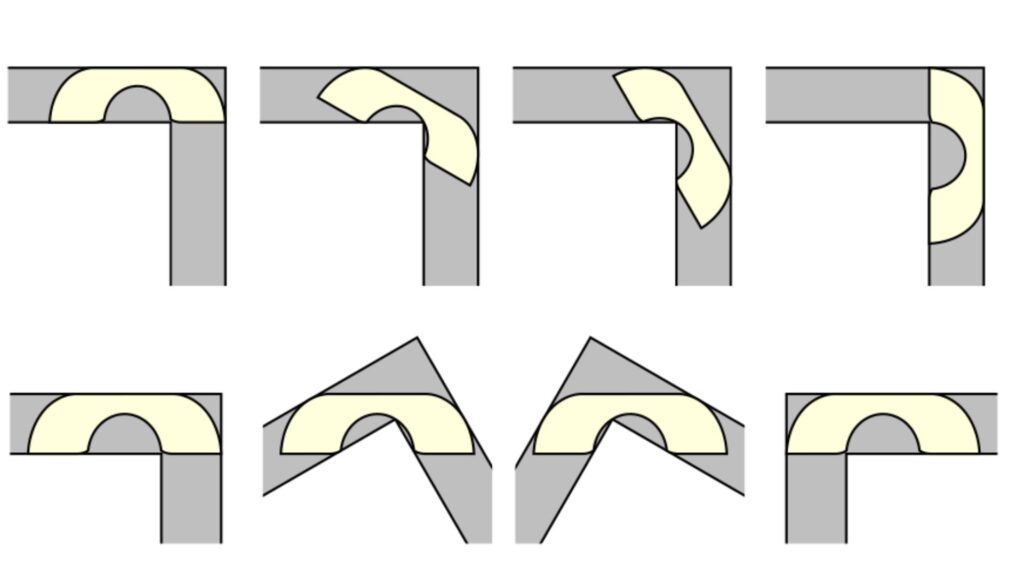
Le problème du canapé, aussi appelé problème du sofa, date de 1966 et se comprend facilement, y compris des non-mathématiciens. Leo Moser, un mathématicien austro-canadien, essaye de trouver la plus grande surface d’un sofa pouvant être déplacé horizontalement dans un couloir large d’une unité et comportant un angle droit.
Mais si la problématique se pose simplement sa résolution est malaisée. C’est un calcul plus compliqué qu’il n’y parait, car il faut réussir à faire correspondre la bonne surface du meuble avec le mouvement que doit exécuter le canapé dans l’espace, en tenant compte des contraintes (l’angle droit et chaque partie du couloir).
Précédemment, avec différentes études, il avait été établi que la surface maximale se situait dans l’intervalle compris entre 2,2195 unités et 2,37 unités.
La borne inférieure de cet intervalle (donc 2,2195) a été démontrée en 1992 par le mathématicien Joseph Gerver, professeur à l’université Rutgers, dans le New Jersay (États-Unis). L’enseignant avait aussi déterminé une forme particulière pour ce canapé : un cube composé d’un creux en demi-cercle et de bords arrondis.
La borne supérieure (2,37) a été trouvée via une méthode assistée par ordinateur en 2018 par Dan Romik et Yoav Kallus, deux mathématiciens travaillant respectivement à l’université de Californie à Davis et celle de Santa Fe, au Nouveau-Mexique.
La solution finale du problème du canapé
Jineon Baek, pour résoudre le problème, repart de la forme du canapé mis au point par Joseph Gerver. Après une centaine de pages de démonstration, il arrive finalement à la réponse suivante : dans un couloir d’une unité de large, la surface maximale possible du canapé est bien celle que Gerver avait trouvée au départ, c’est-à-dire 2,2195 unités.
Sa solution doit encore être vérifiée par différents mathématiciens, mais il se pourrait bien qu’il s’agisse, 58 ans après sa formulation, du clap de fin de ce problème mathématique.
+ rapide, + pratique, + exclusif
Zéro publicité, fonctions avancées de lecture, articles résumés par l'I.A, contenus exclusifs et plus encore.
Découvrez les nombreux avantages de Numerama+.
Vous avez lu 0 articles sur Numerama ce mois-ci
Tout le monde n'a pas les moyens de payer pour l'information.
C'est pourquoi nous maintenons notre journalisme ouvert à tous.
Mais si vous le pouvez,
voici trois bonnes raisons de soutenir notre travail :
- 1 Numerama+ contribue à offrir une expérience gratuite à tous les lecteurs de Numerama.
- 2 Vous profiterez d'une lecture sans publicité, de nombreuses fonctions avancées de lecture et des contenus exclusifs.
- 3 Aider Numerama dans sa mission : comprendre le présent pour anticiper l'avenir.
Si vous croyez en un web gratuit et à une information de qualité accessible au plus grand nombre, rejoignez Numerama+.
Abonnez-vous à Numerama sur Google News pour ne manquer aucune info !
