Les ingénieurs de l’institut de Technion (Israël) ont développé un système informatique capable de générer de nouvelles conjectures mathématiques comme potentiels points de départ de théorèmes.
Une conjecture désigne une proposition mathématique qui n’est pas encore prouvée. Lorsque la conjecture est démontrée, elle se transforme en théorème. Les théorèmes ont une place cruciale en science et peuvent orienter des décennies de découvertes dans différents champs, comme celui de la mathématicienne Emmy Noether sur les lois de la conservation de l’énergie, qui a révolutionné la physique moderne.
La machine développée par ces ingénieurs, fonctionnant avec l’intelligence artificielle et l’automatisation informatique, se base sur les constantes : à l’inverse des variables, ce sont des valeurs qui restent fixes, indépendamment de toute structure et de tout calcul, et que l’on retrouve dans tout domaine, de la physique à la biologie. Le nombre d’or, le nombre d’Euler ou encore le nombre Pi sont des constantes célèbres utilisées bien au-delà des maths.
L’exploit de la machine, The Ramanujan Machine, se situe dans son usage des constantes pour générer des conjectures. Il est rare, dans l’histoire des mathématiques, que des théorèmes aient été bâtis à partir de constantes. Ce fut l’apanage de grands noms de la science, comme un certain Isaac Newton ou encore… Srinivasa Ramanujan (1887-1920), qui donne justement son nom à cette machine. Ce mathématicien indien, peu connu du grand public, est devenu célèbre dans la communauté scientifique à la fin du 19è siècle pour avoir développé des théorèmes à partir des constantes du nombre Pi et du nombre d’Euler.
Ramanujan était si brillant que la majeure partie de ses calculs, même ceux qu’ils a énoncés sans preuve à l’époque, ont été confirmés au fil des décennies, encore bien longtemps après sa mort. « Elles devaient être vraies, car si elles avaient été fausses, personne n’aurait eu assez d’imagination pour les inventer », commentait le mathématicien Godfrey Harold Hardy à propos des équations de Ramanujan.
Une IA peut-elle avoir de l’intuition mathématique ?
« Pendant des siècles, les nouvelles formules mathématiques relatives aux constantes fondamentales ont été rares et généralement découvertes de manière sporadique. De telles découvertes sont souvent considérées comme un acte d’ingéniosité mathématique ou d’intuition profonde par de grands mathématiciens », expliquent les ingénieurs en introduction d’un papier publié dans Nature, le 3 février 2021, pour détailler leurs recherches.
Ils ont essayé de reproduire, informatiquement, cette intuition. Le système puise dans des correspondances entre des valeurs numériques, les nombres au sein même des constantes, pour formuler des conjectures. Cela permet d’aller « dans la structure profonde des constantes ».
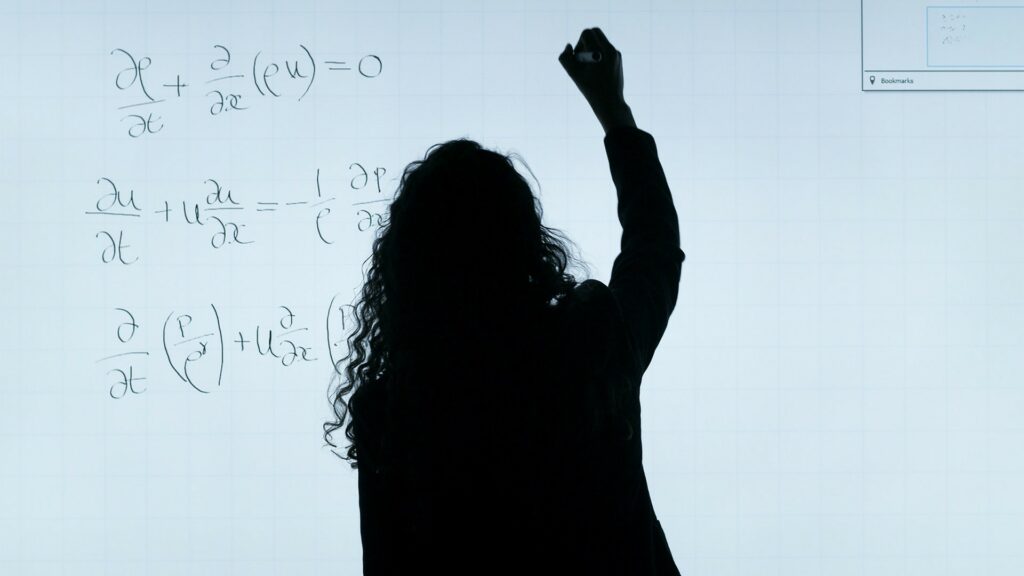
C’est ensuite aux humains d’essayer de prouver les conjectures fournies par la machine. // Source : Pexels
« Nos résultats sont impressionnants parce que l’ordinateur ne se soucie pas de savoir si la preuve de la formule est facile ou difficile, et ne base pas les nouveaux résultats sur des connaissances mathématiques préalables mais seulement sur les nombres au sein des constantes mathématiques, explique le professeur Ido Kaminer. Dans une large mesure, nos algorithmes fonctionnent de la même manière que Ramanujan lui-même, qui a présenté des résultats sans preuve. »
La Ramanujan Machine a déjà permis de trouver des dizaines de formules de conjectures, dont une partie n’était pas encore connue et dont plusieurs sont reliées au nombre Pi et au nombre d’Euler. Si la machine établit les conjectures, elle ne les démontre pas : c’est aux mathématiciens et aux mathématiciennes en chair et en os d’en trouver les preuves, si elles existent. Certaines des conjectures trouvées par la machine ont pu être facilement prouvées, tandis que d’autres restent encore à démontrer (si elles sont vraies).
Les ingénieurs espèrent en tout cas « fournir un outil significatif pour la recherche mathématique ». Ils ont d’ailleurs fondé un site internet de science participative, où le code de la machine est disponible, ainsi que les résultats, et où des mathématiciens et mathématiciennes peuvent proposer des équations visant à résoudre les conjectures encore non prouvées.
+ rapide, + pratique, + exclusif
Zéro publicité, fonctions avancées de lecture, articles résumés par l'I.A, contenus exclusifs et plus encore.
Découvrez les nombreux avantages de Numerama+.
Vous avez lu 0 articles sur Numerama ce mois-ci
Tout le monde n'a pas les moyens de payer pour l'information.
C'est pourquoi nous maintenons notre journalisme ouvert à tous.
Mais si vous le pouvez,
voici trois bonnes raisons de soutenir notre travail :
- 1 Numerama+ contribue à offrir une expérience gratuite à tous les lecteurs de Numerama.
- 2 Vous profiterez d'une lecture sans publicité, de nombreuses fonctions avancées de lecture et des contenus exclusifs.
- 3 Aider Numerama dans sa mission : comprendre le présent pour anticiper l'avenir.
Si vous croyez en un web gratuit et à une information de qualité accessible au plus grand nombre, rejoignez Numerama+.
Si vous avez aimé cet article, vous aimerez les suivants : ne les manquez pas en vous abonnant à Numerama sur Google News.
