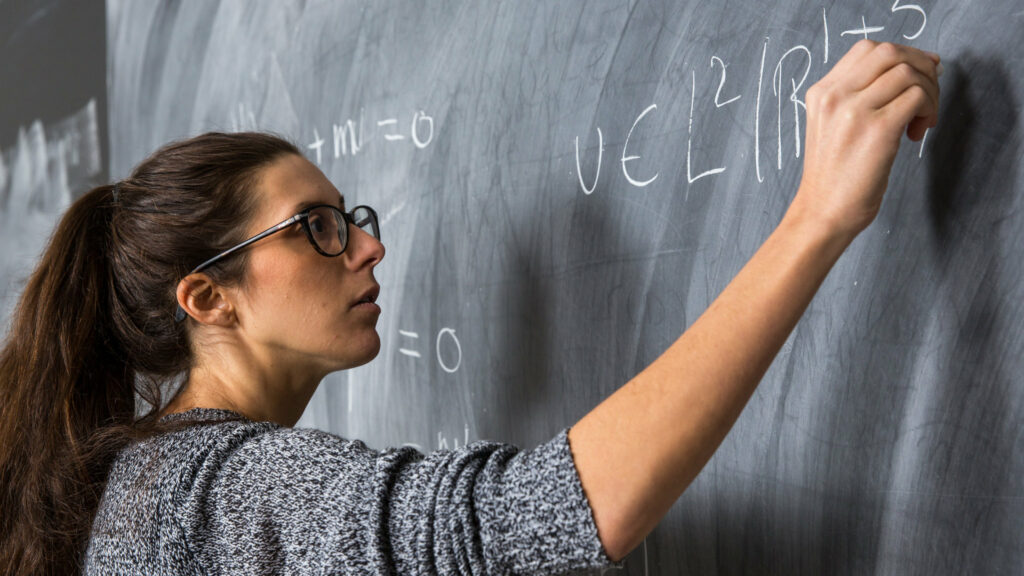La scène se passe en Finlande, au milieu de l’hiver. Alors que dehors il neige, je lis et relis mon cahier de brouillon dans mon bureau bien chauffé. Je n’arrive pas à croire ce que j’ai écrit moi-même plus tôt dans la journée.
Aurais-je trouvé la solution à un problème ouvert depuis plus de vingt ans ? Non, c’est impossible. Pourtant j’ai beau relire, je ne vois pas d’erreur. Mon cœur s’emballe alors que je tourne les pages de mon cahier, sans trouver la moindre faille dans mon raisonnement.
N’osant y croire, je me lève pour aller montrer tout ça à mon directeur de thèse, avant de crier complètement victoire… Je toque à son bureau, et même si je vois bien que je l’interromps, il me propose de lui expliquer mon idée au tableau.
Au bout de quelques minutes à peine, il m’explique patiemment que je n’ai pas bien compris la définition… et donc que ce que j’ai fait ne sert strictement à rien. Encore raté. Pour la troisième fois… de la semaine.
L’euphorie fait place à une déception mêlée de honte d’avoir une nouvelle fois dérangé mon directeur de thèse pour rien. Certes, ces étapes ne se succèdent pas toujours à une telle vitesse, mais cet exemple illustre à merveille combien les montagnes russes émotionnelles rythment mon quotidien de chercheur, dans une succession de hauts et de bas.
Mais pourquoi tu fais ça ?
Quand j’explique à quelqu’un que je suis chercheur en mathématiques et informatique, la première question ressemble souvent à : « mais c’est vraiment un métier ça ? ». Suivie de près par la seconde : « Mais à quoi ça sert ? Pourquoi quelqu’un voudrait-il faire des maths toute sa vie ? ! »
La réponse immédiate à cette deuxième question est valable pour toutes les sciences fondamentales : certaines découvertes ne peuvent être faites qu’en cherchant sans but. L’exemple le plus courant est celui du laser, dont les bases théoriques ont été découvertes par Einstein en 1917. Initialement sans application, on l’a qualifié pendant un moment de « solution cherchant un problème à résoudre ».
Aujourd’hui, c’est devenu un élément indispensable dans de très nombreuses technologies : en médecine, météo, énergie nucléaire, mesures en tout genre…
En mathématiques et en informatique aussi, la recherche fondamentale est… fondamentale. Elle permet de développer des méthodes et des outils mathématiques qui, s’ils n’ont aucun autre intérêt immédiat que de satisfaire la curiosité d’une poignée de mathématiciens et mathématiciennes, serviront peut-être comme base pour un développement majeur en informatique ou en physique. Ou peut-être pas.
Une partie de cette recherche ne servira sans doute jamais à rien, mais il faut prendre ce « risque » pour donner un socle aux nouvelles découvertes ayant plus d’applications. Le but final est tellement flou et à si long terme que je n’ai aucune assurance que mes travaux auront une application de mon vivant – ni même d’application tout court.
Un métier rempli de surprises
Alors qu’est-ce qui me motive à me lever chaque jour ? Ce sont justement ces montagnes russes émotionnelles. Quand je me mets devant une feuille blanche pour m’attaquer à un problème, je ne sais pas vraiment combien de temps cela va me prendre ni même si je vais y arriver. Cette incertitude est à la source de ce que je considère comme la première qualité de mon métier : la surprise, qui est aussi à la source des nombreuses émotions qui interviennent dans la recherche.
Enfin, les innombrables aller-retour avec mon directeur de thèse ont fini par s’achever. Même si nous n’avons pas pu résoudre ce problème ouvert depuis si longtemps, mes nombreux faux espoirs et sa patience ont abouti à un résultat intéressant, ce qui teinte a posteriori tous ces va-et-vient d’une note de fierté.
Des problèmes qui résistent
Évidemment, ce genre d’aller-retour ne se termine pas toujours aussi bien. J’ai entamé beaucoup de travaux que j’ai ensuite laissés de côté « pour plus tard », ne sachant pas vraiment si j’allais m’y remettre un jour. Quand cela fait des semaines ou des mois qu’un problème résiste, sans parfois même montrer un signe de faux espoir, il est difficile de garder la motivation de s’y attaquer tous les jours, et il finit souvent par être délaissé.
Parfois, la fin est plus violente : il m’est arrivé de me rendre compte que je me trompais tellement que rien de ce que j’avais fait ne pouvait être sauvé. Dans ce cas, on est énervé, surtout contre soi-même, de ne pas avoir vu plus tôt qu’on s’était lancé sur une mauvaise piste, ou pire, d’avoir mal compris quelque chose qui maintenant nous semble évident.
Dans ces moments-là, on s’en veut tellement qu’il est parfois difficile de prendre du recul, et de se rendre compte que c’est justement parce qu’on a « gâché » quelques semaines à mal comprendre, qu’on a fini par assimiler ce qui semble maintenant une évidence.
Une large palette d’émotions
Et si les autres tâches de mon métier de chercheur sont relativement prévisibles et fixées à un moment précis – rendez-vous, tâches administratives, enseignements, rendus d’article, exposé devant des collègues –, elles présentent tout de même leur lot de surprises.
La joie, évidemment, quand un article scientifique qui a mis des mois à naître est accepté dans une revue prestigieuse.
Ou la déception, quand ce même article se voit refusé.
Suivie de l’incompréhension quand les raisons du refus sont peu claires, ou de l’énervement quand elles semblent infondées.
Ou encore la fierté de constater qu’une personne dans l’audience écoute encore attentivement à la fin d’un long exposé.
Les maths, une forme d’art ?
L’imaginaire populaire perçoit bien souvent les mathématiques comme une discipline radicalement opposée à celles de l’art. Je considère au contraire qu’elles y sont tout à fait liées, lorsque l’on connaît la large palette d’émotions qu’elles sont capables de mobiliser.
Ce constat me semble d’autant plus vrai que toutes ces émotions peuvent être partagées. Nous travaillons souvent à plusieurs chercheurs et chercheuses sur un problème, et parcourons donc ensemble ces montagnes russes. Sans parler des émotions qui nous traversent en lisant ou en écoutant le travail des autres : émerveillement, admiration, dégoût ou jalousie… À l’inverse, il nous est donc possible de susciter toutes ces émotions chez les autres à travers nos travaux de recherche.
Libérez les mathématiques !
L’expérience que je décris surprendra peut-être les lecteurs et lectrices qui n’ont été confrontés aux maths qu’à travers l’expérience, parfois traumatisante, de l’enseignement prodigué tout au long du parcours scolaire.
Beaucoup d’entre elles n’ont pas eu la chance d’y voir autre chose que de la frustration ou de l’incompréhension. Dans la grande majorité des cas, l’enseignement des maths ne laisse en effet que peu de place à la créativité ou à l’exploration, très présente en recherche.
C’est un problème que le mathématicien Paul Lockhart aborde en profondeur dans son essai « A Mathematician’s Lament », traduit en français sous le nom de « Libérez les mathématiques ! »
L’euphorie de la découverte
J’ai eu la chance d’expérimenter l’euphorie de la « découverte » mathématique assez tôt pendant mes études.
Dans le cadre d’un « projet encadré », je me suis retrouvé à étudier mathématiquement les solutions d’un petit jeu de société. Après quelques recherches sur Internet, j’en étais venu à la conclusion que personne n’avait vraiment étudié ce problème, il allait donc falloir que je fasse quelque chose de complètement nouveau.
Après plusieurs semaines à tourner en rond, rien ne marchait. J’y pensais tout le temps, dès que mon esprit était libre, il fallait qu’il se retourne vers ce problème. Au bout d’un moment, comme un déclic : « Et si… ? » Sans même me lever de mon lit, j’écris rapidement ce que j’avais en tête, et… ça marche ! Quelle euphorie de résoudre un problème sur lequel on planchait depuis si longtemps, et surtout, que personne n’avait encore jamais attaqué !
Bon, j’ai aussi découvert plusieurs années après que ce jeu avait en fait été étudié sous tous les angles depuis de nombreuses années, et que ce que j’avais fait n’avait absolument rien de nouveau. Mais tant qu’on ne sait pas que ça existe déjà, toute trouvaille a le goût de la découverte.
C’est cette expérience qui m’a poussé à aller voir au-delà du formalisme mathématique, qui peut sembler froid et rigide au premier abord, pour y voir toute la beauté qui s’y cache.
Avec le recul, je crois que je suis tout de suite devenu accro à cette sensation grisante lorsqu’on résout un problème, et c’est ce qui m’a poussé à en faire mon métier. À bien y réfléchir donc, ce que je cherche vraiment au quotidien n’a rien à voir avec des équations. Toute mon énergie est consacrée à ne jamais sortir des rails de ces montagnes russes émotionnelles.![]()
Etienne Moutot, Centre national de la recherche scientifique (CNRS)
Cet article est republié à partir de The Conversation sous licence Creative Commons. Lire l’article original.
+ rapide, + pratique, + exclusif
Zéro publicité, fonctions avancées de lecture, articles résumés par l'I.A, contenus exclusifs et plus encore.
Découvrez les nombreux avantages de Numerama+.
Vous avez lu 0 articles sur Numerama ce mois-ci
Tout le monde n'a pas les moyens de payer pour l'information.
C'est pourquoi nous maintenons notre journalisme ouvert à tous.
Mais si vous le pouvez,
voici trois bonnes raisons de soutenir notre travail :
- 1 Numerama+ contribue à offrir une expérience gratuite à tous les lecteurs de Numerama.
- 2 Vous profiterez d'une lecture sans publicité, de nombreuses fonctions avancées de lecture et des contenus exclusifs.
- 3 Aider Numerama dans sa mission : comprendre le présent pour anticiper l'avenir.
Si vous croyez en un web gratuit et à une information de qualité accessible au plus grand nombre, rejoignez Numerama+.
Toute l'actu tech en un clin d'œil
Ajoutez Numerama à votre écran d'accueil et restez connectés au futur !

Marre des réseaux sociaux ? Rejoignez la communauté Numerama sur WhatsApp !