ZIP, JPEG, streaming… : comment fonctionne la compression de données ?

Si vous tentiez de pitcher la série Silicon Valley comme « les tribulations d’une startup spécialisée dans la compression de données », cela ne sonnerait pas très sexy. Mais si vous suivez comme nous les aventures de Pied Piper, vous savez que la compression est en réalité un domaine vital de la tech aux applications omniprésentes.

Mais avant toute chose, infligeons-nous une première désillusion : non, le « score de Weissman » n’existe pas en vrai. Il n’y a pas de méthode universelle et absolue pour quantifier la puissance d’un algorithme de compression ; seulement des benchmarks, un peu comme pour les microprocesseurs. Voilà, c’est dit. Place à la vraie compression.

Entropie et information

Pendant la Seconde guerre mondiale aux États-Unis, un jeune thésard en mathématiques des laboratoires Bell s’attaquait à ce qui allait devenir un des piliers de l’informatique. L’Américain Claude Shannon a bâti sa théorie de l’information sur un concept nommé entropie, qui ici signifie simplement « quantité d’information ». Vous lancez une pièce, vous notez le résultat qui est soit pile, soit face : ça fait un bit d’entropie. Vous faites pareil avec deux pièces : deux bits d’entropie. Vous lancez une pièce et trichez en notant deux fois son résultat : ça reste un bit.

La chaîne de caractères « aaaaaaaaaaaaaaaa » a un taux d’entropie très faible, car elle se résume à « 16 fois a ». Au contraire, « 1f08c6e13b954f80 » a un taux d’entropie élevé, car chaque caractère est complètement aléatoire. Si vous avez fait de la physique, vous vous souvenez peut-être que l’entropie y désigne la « quantité de désordre », et vous remarquerez que la chaîne de caractères aléatoire, par définition complètement désordonnée, est celle ayant le plus d’entropie. Quand il y a peu d’entropie, c’est qu’il y a de l’ordre et de la logique, sous forme de motifs prévisibles.

Détail de la fractale de Mandelbrot, dont la complexité de Kolmogorov est très faible, car elle se résume à une équation de niveau Terminale S. CC Wikimédia

De cette idée ressort la complexité de Kolmogorov, qui représente la longueur de texte (ou de code) la plus courte pour obtenir un résultat donné. Si la manière la plus courte d’écrire « aaaaaaaaaaaaaaaa » est « 16 fois a », cette chaîne de caractère est, selon Kolmogorov, beaucoup moins complexe que « 1f08c6e13b954f80 », dont la manière la plus courte de l’écrire est… « 1f08c6e13b954f80 ».

Vous voyez peut-être où on veut en venir : compresser un fichier, ça veut dire l’écrire de la manière la plus courte possible, en y cherchant les motifs logiques. On comprend vite qu’il y a une limite à la compression sans perte. Si on veut garder toute l’information (entropie) sans en perdre une miette, le résultat compressé ne doit pas avoir moins d’entropie (information) totale que n’en avaient les données initiales. Et vu que la complexité de Kolmogorov correspond à la manière la plus courte d’écrire un fichier, un fichier compressé ne peut pas être plus petit que sa complexité de Kolmogorov. C’est tout bête, n’est-ce pas ?

Compresser un fichier, ça veut dire l’écrire de la manière la plus courte possible

Un sentiment indescriptible…

Le soucis avec la complexité de Kolmogorov est qu’il est impossible de la déterminer systématiquement. En d’autres termes — et heureusement pour nos amis fictifs de Pied Piper — on ne peut généralement pas regarder un fichier compressé et dire sans se tromper s’il peut ou non être encore plus compressé. La démonstration tient dans le paradoxe de Berry, décrit par un libraire d’Oxford au tournant du XXe siècle.

Prenons la phrase « le plus petit entier positif non définissable en moins de treize mots », dont il se trouve qu’elle définit un certain entier positif. Réfléchissez un peu. Vous voyez le problème ?

CC Simon Q

« Le₁ plus₂ petit₃ entier₄ positif₅ non₆ définissable₇ en₈ moins₉ de₁₀ treize₁₁ mots₁₂ » vient d’être défini en douze mots. Monsieur Kolmogorov le comprimerait en combien de mots, du coup ? Douze ou au moins treize ? Avouez que c’est ballot. C’est comme l’expression « sentiment indescriptible » : comment ce sentiment peut-il être indescriptible alors qu’on vient de le décrire avec l’adjectif « indescriptible » ?

Même le meilleur algorithme du monde ne pourra pas tout compresser ; il existera toujours des fichiers qui grossiront une fois passés à la moulinette. C’est logique : on pourrait sinon demander à l’algorithme de compresser le fichier plusieurs fois de suite, et faire rapetisser le fichier jusqu’à ce qu’il disparaisse — tout ça en conservant évidemment toute l’information qu’il y a dedans. L’« algorithme de compression magique » n’existe pas, et en général, compresser un fichier deux fois de suite donne un résultat plus volumineux que le fichier de départ.

Il existe des algorithmes de compression généralistes, comme celui du ZIP, qui marchent relativement bien, quel que soit le fichier qu’ils compriment. Mais pour atteindre de meilleures performances, il vaut mieux choisir des algorithmes spécialisés ; un algorithme calibré pour compresser de l’audio pourrait avoir du mal à faire de même avec de la vidéo. De même, on ne va pas forcément choisir les mêmes algorithmes d’une vidéo à l’autre : une retransmission sportive nécessite de retranscrire fidèlement les mouvements, mais moins les couleurs tandis qu’un documentaire animalier se doit plus d’afficher de belles couleurs que d’être précis dans les mouvements.

Perte ou pas perte ?

Il y a deux grands types de compression : sans perte (lossless) ou avec perte (lossy). La compression sans perte est celle qu’on a étudiée avec Kolmogorov : quand vous zippez et dézippez un fichier, vous voulez que le fichier soit entier à l’arrivée et qu’il n’en manque pas un bout. Toute l’entropie doit être là. Mais pour l’image, le son ou la vidéo, il n’est pas si vital de conserver chaque petit détail qui ne sera de toute façon pas perçu par les sens humains. Chez les images fixes, le JPEG est un codec de compression avec perte, mais qui permet de réduire un fichier à un dixième de sa taille initiale sans modification visible de qualité. Le PNG, au contraire, est un codec sans perte qui fait des fichiers plus gros.

Mais qu’est-ce qu’un codec, demanderez-vous ? Codec est l’abréviation de « codeur-décodeur » : comme son nom l’indique, c’est un petit logiciel dont la fonction est de coder ou de décoder un flux de données. Les codecs audio ont ainsi pour rôle de prendre un fichier audio (écrit en bits) et de le convertir en signal analogique (c’est-à-dire du « vrai son »), et inversement — en effectuant généralement de la (dé)compression au passage.

CC Brett Lessard

Pour continuer dans les exemples audio, un des principaux codecs sans perte est le FLAC (Free Lossless Audio Codec), qui est capable de comprimer à 50-60 % et a le mérite d’être libre de droits. L’ALAC (Apple Lossless Audio Codec) est identique dans les faits, à ceci près qu’il n’est généralement pas supporté par Android. On compte aussi les fameux codecs WMA de Microsoft, dont trois sont avec perte et un sans perte.

Mais codec n’est pas synonyme de format. Un fichier de format AVI de chez Microsoft contient à la fois de l’audio et de la vidéo, qui sont gérés par deux codecs différents. L’AVI est ainsi ce qu’on appelle un format conteneur, au même titre que le WAV (également de Microsoft), le FLV (d’Adobe), le MP4 (du Moving Picture Experts Group) ou encore l’Ogg (des libristes de Xiph.org).

Un des plus célèbres formats compressés, le ZIP utilise le plus souvent l’algorithme DEFLATE. C’est lui que nous allons étudier en tant qu’algorithme de compression sans perte. DEFLATE marche en deux temps : il effectue d’abord de la compression par dictionnaire, et ensuite fait du codage entropique.

Le ZIP, partie 1 : compression par dictionnaire avec Lempel-Ziv

C’est le b.a.-ba de la compression, à tel point que comme Monsieur Jourdain, on en fait tous les jours sans le savoir. Le run-length encoding (RLE) est le plus basique : si on rencontre la séquence « aaaaaaaaaaaaaaaa » de tout à l’heure, au lieu d’écrit chacun des seize a, on écrit « 16a » et on gagne treize caractères de place. De même, un vieil algorithme de compression d’image pourrait dire « 50 pixels noirs » au lieu d’écrire « pixel noir » cinquante fois de suite — on dit « vieux », car les images qu’on trouve de nos jours sur nos écrans Full HD ont presque toujours des variations de nuance d’un pixel à l’autre, ce qui enlève l’intérêt d’un RLE.

CC Jonathan Cohen

Le même principe se retrouve de façon plus élaborée chez les algorithmes LZ77 et LZ78 déposés par les chercheurs Lempel et Ziv en 1977 et 1978 respectivement. Ceux-ci sont à la base de toute la compression par dictionnaire. Quand vous dites « UE » à la place de « Union européenne », « NASA » pour « National Aeronautics and Space Administration » ou « MP3 » pour « MPEG-2 Audio Layer III », vous faites plus ou moins de la compression LZ78 : au lieu de répéter dans toute leur longueur ces noms redondants, vous les stockez dans un petit dictionnaire (en l’occurrence dans votre tête) et vous y référez grâce à des « indices » uniques et simples (en l’occurrence des acronymes). Dans la pratique, LZ78 constitue son dictionnaire au fur et à mesure de la compression et y note un peu tout et n’importe quoi ; mais le principe est le même.

LZ77, lui, n’a pas de dictionnaire séparé, mais fonctionne avec une « fenêtre glissante » de données qui lui permet de se souvenir quand était la dernière fois qu’il a vu tel ou tel motif. Il dit alors « c’est le même motif que celui qui se trouve il y a X bits et qui dure Y bits », et ça compresse. C’est le LZ77 que DEFLATE utilise.

Le ZIP, partie 2 : codage entropique avec notre ami Huffman

La compression par dictionnaire étant un peu facile, on va passer au sérieux avec le codage entropique. Ce terme désigne tout un paquet de techniques de compression sans perte qu’on qualifierait de « généralistes », qui marchent bien dans tous les cas.

La première technique de codage entropique est le codage de Huffman, mis au point par un thésard du MIT en 1952 et qui est utilisé dans les fichiers ZIP. Pour simplifier l’explication, on suppose qu’on veuille compresser un texte écrit en caractères ASCII (c’est-à-dire où chaque caractère correspond à un octet, soit huit bits). C’est un peu bête de devoir réécrire chacun des huit mêmes bits « 01100101 » à chaque fois qu’on veut noter une lettre fréquente comme le e. N’y aurait-il pas moyen de faire plus court ?

Ce que Huffman a fait, c’est qu’il a pris toutes les lettres du texte et les a rangées dans des tiroirs numérotés de haut en bas, les lettres les plus rares en bas du meuble et les plus fréquentes en haut. En vrai, c’est censé être ce qu’on appelle un arbre de Huffman, mais on vous passe les détails de la construction. Quand l’algorithme de compression verra la lettre e, il écrira simplement le numéro du tiroir : « 1 ». Et quand il verra la lettre x, il écrira par exemple « 10110 » (soit « 22 » en binaire).

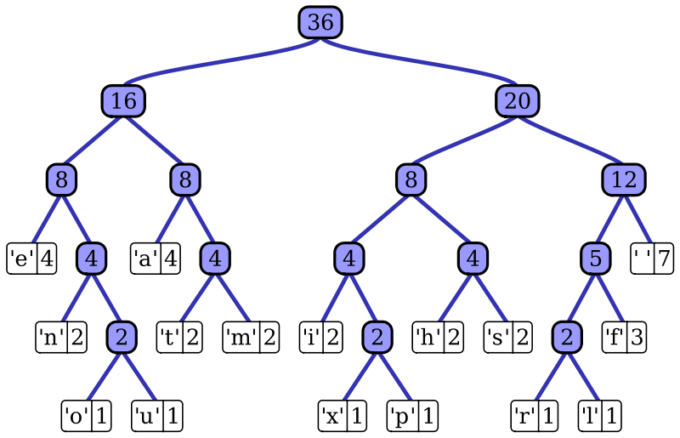
Dans la vraie vie, le meuble à tiroirs s’appelle « arbre », est pyramidal, et les « 1 » et « 0 » disent si le tiroir est à gauche ou à droite. Source : Wikimédia

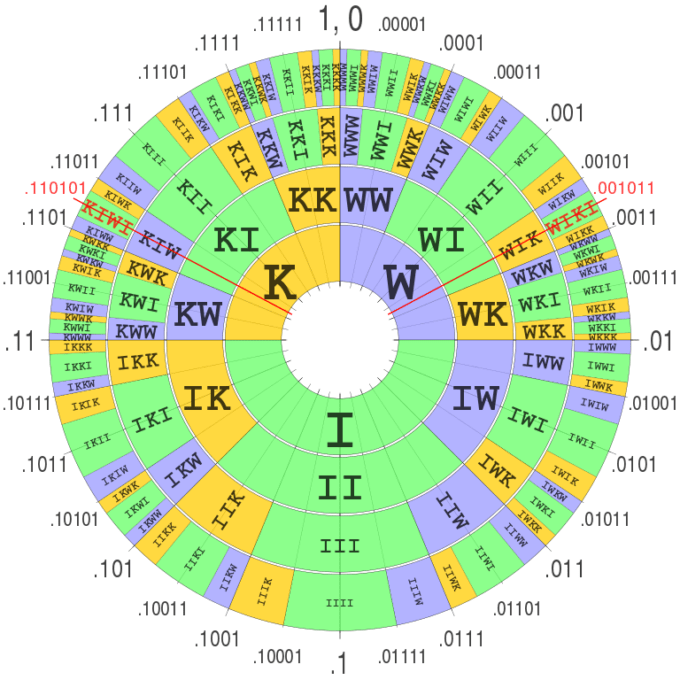
Plus populaire que le codage de Huffman, le codage arithmétique est certes un peu plus long à mettre en place, mais compresse souvent mieux. Le principe général est le même, mais au lieu de coder chaque symbole séparément, c’est comme si tous les textes possibles et imaginables étaient en théorie répertoriables sur un immense cadran comme celui-ci :

Source : Wikimédia

Il « suffit » de construire le texte sur le cadran, de pointer l’aiguille du cadran dessus, et de lire l’angle ; ce dernier correspond au texte compressé. Ce concept étant déjà plus compliqué, retenez juste celui de Huffman, c’est largement suffisant pour comprendre. Enfin, le codage par intervalle ressemble beaucoup au codage arithmétique, sauf qu’il ne fonctionne pas nécessairement en base binaire, mais dans la base qui lui est la plus pratique (au hasard, une base 28 pour comprimer toutes les lettres de l’alphabet plus l’espace et le point).

Compression avec perte : le JPEG

Le JPEG va nous servir d’exemple pour la compression avec perte. D’abord, l’algorithme JPEG diminue la résolution de la chrominance, à laquelle l’œil humain ne fait pas trop attention. Ça s’appelle le sous-échantillonnage.

Ensuite, l’algorithme découpe l’image en carrés de 8 pixels et y applique une transformée en cosinus discret. Pour parler poétiquement, c’est comme si le bout de fichier était transformé en ondes sonores ou en vaguelettes sur l’eau. La prochaine étape, la quantification, est celle où on peut faire jouer un degré de compression plus ou moins élevé. Les « vagues » sont cartographiées de manière simplifiée : au lieu de redessiner exactement les courbes, on n’en note que quelques points. Moins il y a de points, moins c’est précis, et plus c’est compressé.

La quantisation terminée, le JPEG prend sa carte et la passe par deux étapes de codage entropique (qui n’a maintenant plus de secret pour vous) : un bête RLE — mais qui lit le bout de carte en zigzag, ne rigolons pas — et un codage de Huffman. Voilà, c’est réglé !

La plupart des algorithmes de compression avec perte, y compris ceux qui travaillent en audio, utilisent une forme de transformée en cosinus direct. Malgré les artéfacts qu’elle génère et qu’on a tous pu voir sur un GIF ou une vidéo de mauvaise qualité, la compression avec perte peut parfois avoir des effets souhaitables. En audio, elle a ainsi tendance à adoucir les pics de volume — ce qui permet, par exemple dans un morceau de musique classique, que les passages piano joués doucement soient encore audibles même sur le bruit de fond d’une voiture.

En pratique : le streaming vidéo

Le streaming vidéo, un des principaux fonds de commerce fictifs de Pied Piper, a fait ses débuts sur le vrai Internet le 24 juin 1993. Le groupe de garage rock Severe Tire Damage, originaire de Palo Alto dans la Silicon Valley, faisait une prestation dans le fameux centre de recherche Xerox PARC. Les chercheurs discutaient à ce moment-là de la technologie de retransmission qu’ils venaient de mettre au point. L’idée était toute trouvée : pourquoi ne pas exposer le fruit des recherches du Xerox PARC en retransmettant le concert en live sur Internet ?

https://youtube.com/watch?v=HRa2pE5-Ny0

Le résultat — une vidéo de 152 par 67 pixels saccadée à 8-12 images par seconde, avec une qualité sonore digne « au mieux [d’une] mauvaise liaison téléphonique » — aurait « aspiré la moitié de la bande passante d’Internet tout entier ».

Les flux audio et vidéo sont encodés avec les codecs adéquats, passés dans un conteneur dit « bitstream » comme le MP4 ou le FLV, envoyés via les tuyaux de l’Internet grâce à un protocole de transport comme le RTP d’Adobe, et décodés chez l’utilisateur avec les mêmes codecs. Par exemple, si les keynotes d’Apple refusent d’être retransmises sur un autre navigateur que Safari ou Microsoft Edge, c’est à cause du protocole de transport utilisé : HLS (HTTP Live Streaming), certes open source et implémenté par toute une gamme de lecteurs vidéo (dont VLC), mais que ni la version desktop de Google Chrome ni Mozilla Firefox ne supportent nativement.

Le fichier est découpé en plusieurs blocs, dupliqués et compressés à des degrés différents

Si votre connexion 4G flanche alors que vous regardez une vidéo sur YouTube, plutôt que de figer (voire saccader) la vidéo le temps que le réseau revienne, on peut partiellement y pallier en envoyant un flux vidéo plus compressé. C’est ce qu’on appelle le streaming à bitrate adaptatif : avant envoi, le fichier est découpé en plusieurs blocs, dupliqués et compressés à des degrés différents, de sorte que le protocole puisse choisir des blocs dont la compression est adaptée à la connexion.

Sur les flux vidéo, et même sur les fichiers vidéo tout court, il faut gérer un compromis temps-mémoire. L’algorithme de compression vidéo aura beau être excellent, il ne sera pas utilisable si la décompression met trop de temps pour être faite à la volée, auquel cas l’image ne tiendra pas le rythme comme par mauvaise connexion réseau.

Proposez une nouvelle stratégie de pivot !

On vous a expliqué que le principe de la compression sans perte était d’essayer de trouver une logique dans le contenu du fichier. Un excellent algorithme de compression aurait également une autre fonction particulièrement utile, absolument pas liée au fait de rendre les choses plus petites, rapides ou efficaces. À votre avis, laquelle est-ce ?

Alexa, l’IA commerçante d’Amazon

Un excellent algorithme de compression est également une excellente intelligence artificielle, et inversement. Bien que les algorithmes qu’on a vus dans cet article ne sont pas très futés, l’apprentissage par machine a le même but de détection et de prévision des motifs. Un algorithme de compression de texte, qui pousserait son analyse jusqu’à comprendre toutes les variations sémantiques et flexions grammaticales de ses données, pourrait théoriquement être reconverti en chatbot. Dans l’autre sens,  Google a travaillé sur une IA de compression d’images, et Netflix a de même mis au point une IA pour compresser ses films.

Maintenant que vous avez découvert que vous êtez (presque) un algorithme de compression vivant, votre formation express est terminée. Il ne vous reste plus qu’à déposer votre CV dans la boîte mail de Pied Piper et à leur proposer de pivoter vers le domaine de l’IA au cas où leur initiative du moment se terminerait en catastrophe industrielle.

Pour ceux qui seraient intéressés par la lecture d’un vrai article scientifique écrit spécialement pour la réalisation de Silicon Valley, le papier « Optimal Tip-to-Tip Efficiency » du mathématicien Vinith Misra explique très sérieusement en 12 pages, équations et schémas à l’appui, le génial final de la saison 1. On vous prévient d’abord du spoiler, et aussi que c’est du contenu NSFW (not safe for work) — pas vraiment adapté à tous les âges.